[윤복원의 물리상식으로 푸는 요즘 세상]
둥그런 지구 위에서의 수평은 볼록한 모양이지만
회전으로 만든 인공중력에서 수평은 오목한 모양
둥그런 지구 위에서의 수평은 볼록한 모양이지만
회전으로 만든 인공중력에서 수평은 오목한 모양

‘어느 쪽으로도 기울어져 있지 않다’는 의미의 ‘수평’은 중력과 밀접한 관련이 있다. 픽사베이

‘수평’이 ‘평평하다’라는 것을 의미할까? 수평인 당구대 표면은 적어도 눈에 보이기에는 평평하다. 하지만 ‘수평이다’라는 것이 항상 ‘평평하다’는 것을 의미하지는 않는다. 조그만 연못에 있는 잔잔한 물의 표면은 평평하게 보일 수 있다. 하지만 바다와 같이 매우 넓은 곳에서는 물이 아무리 잔잔하더라도 더 이상 평평하다고 말하기 곤란하다. 지구 자체가 공모양이기 때문이다. 지구가 끌어당기는 중력의 크기는 지구 표면 어디에서도 거의 같지만, 중력의 방향은 지구의 어느 곳에 있느냐에 따라 많이 변하기도 한다. 예를 들어, 대한민국 서울의 지구 정반대에 위치한 남미의 대서양 바다에서는 중력의 방향이 서울과는 완전히 반대다. 평균 지름이 1만2742km인 지구에서는, 한쪽 방향으로 111.2km 갈 때마다 중력의 방향이 1°씩 변한다. 111.2km의 90배인 1만km 떨어지면 중력의 방향은 90° 꺾인다. 180배인 2만km 떨어진 곳은 지구 중심을 가로질러 있는 지구 정반대 지점이어서 중력의 방향은 완전히 반대 방향이다. 같은 한국 땅에서도 중력의 방향이 적지 않게 변한다. 서울과 부산 사이의 직선 거리는 약 325km다. 이 정도 거리에서 중력방향은 2.92°만큼 변한다. ‘그림 1’처럼 한반도를 가로지르는 아주 긴 그리고 완벽하게 평평한 평면을 만들었다고 가정해 보자. 그 평면의 가운데를 서울에 놓고 한쪽 끝은 부산을 향하게 한 다음, 수평계를 사용해서 평면의 서울 부분을 수평으로 맞춘다고 하자. 그러면 그 평면의 부산쪽 끝 부분도 수평일까? 부산에 있는 한쪽끝의 평면은 수평과 비교해 2.92°만큼 기운다. 부산에서의 중력 방향이 서울에서와는 2.92°만큼 차이가 있기 때문이다. 기운 방향은 서울을 향한다. 만약에 부산 쪽에 있는 평면 위에 공을 올려놓으면 공은 기울어진 평면을 따라 서울 방향으로 저절로 굴러 간다. 반면 서울 쪽의 평면은 수평으로 맞춰져 있으니 공을 올려놔도 저절로 굴러가지 않는다. 수평으로 맞춘 서울 쪽 평면이 서울의 땅바닥에 놓여 있다면 부산에서 이 평면은 8300m 더 높은 곳에 위치한다.
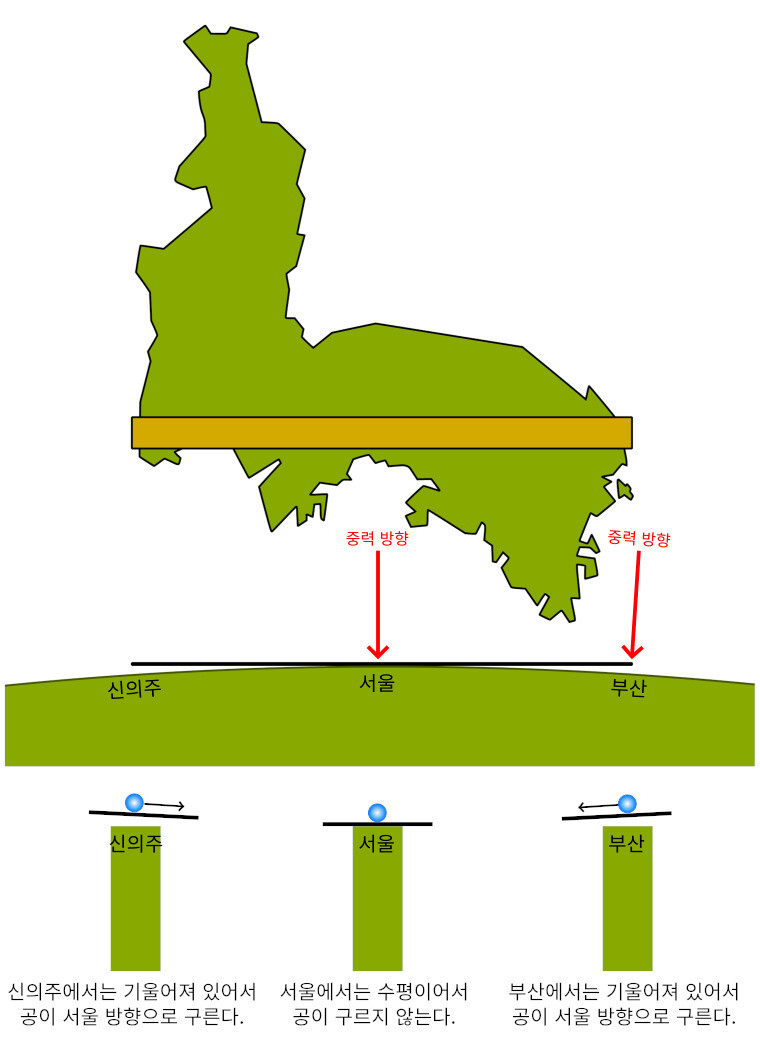
그림 1. 한반도를 가로지르는 가상의 완벽한 평면을 만들어 서울 쪽 위치에서 수평을 맞춘 경우: 부산에서 이 평면은 수평에서 2.92° 기운다. 서울 쪽 평면은 수평이어서 가만히 놓은 공은 어디로도 굴러가지 않는다. 하지만 부산 쪽 평면은 서울을 향해 기울어서 공이 서울 방향으로 굴러간다.
수평인 면이 완벽하게 평평하려면? 완벽하게 평평하면서 수평이기도 한 표면은 어떤 걸까? 평평한 표면 위의 어디에서나 수평이라는 것은 중력의 방향이 어디에서도 표면에 직각인 아래방향으로 향해야 한다는 얘기다. 이런 것이 가능한 경우의 하나가 무한히 평평한 표면이다. 우주 어디에도 이런 곳은 존재하지 않지만, 상상으로는 이런 천체구조를 생각해 볼 수 있다. 이런 천체구조 위에서 지구 위의 중력과 같은 크기의 중력이 만들어지려면 그 두께가 얼마나 되어야 할까? 부피당 질량, 다시 말해 질량 밀도가 지구의 평균 질량밀도와 같다고 가정하면, 두께가 4240km이어야 한다. 만약 질량밀도가 지구 껍데기인 지각의 평균 질량밀도와 같다면, 그 두께는 9000km이어야 한다. 이런 상상의 평평한 천체 구조 위에서의 중력은 지구 위에서와는 다른 특징이 있다. 높이와 관계없이 중력의 크기가 줄어들지 않고 일정하다. 따라서 아무리 높이 올라가도 중력을 벗어날 수 없다. 이런 곳에서는 인공위성도 불가능하다. 추진력 없이 상공에 있을 수 있는 궤도 자체가 존재하지 않기 때문이다. 대기가 존재한다면 양력을 이용한 비행기로 하늘을 나는 정도는 가능하다.
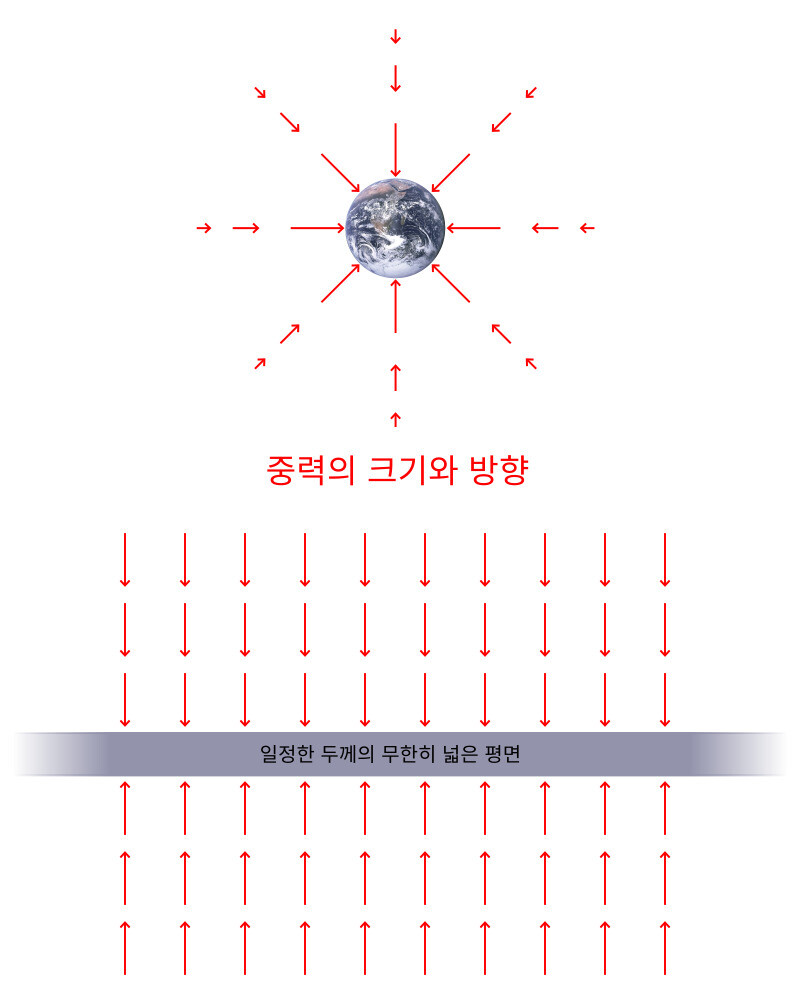
그림 2. (위)지구에서는 수평인 표면이 공모양으로 볼록한 모양이다. 중력의 방향은 지구 중심을 향하는 방향이고, 중력의 크기는 지구에서 멀어질수록 작아진다. (아래) 무한히 넓은 평면에서 중력의 방향은 어디에서도 평면에 수직인 방향이고, 중력의 크기는 평면에서 멀어져도 변하지 않는다.
인공중력으로 만드는 오목한 수평 지표면의 모든 위치에서 수평인 면을 모아 연결하면 지구 모양과 같은 공 모양이 된다. 수평인 표면이 볼록하다는 얘기다. 수평이 오목한 경우도 있을까? 인공중력을 만들면 수평이 오목한 모양이 되는 것이 부분적으로 가능하다. 지구 주위를 로켓 추진없이 도는 우주정거장 안에서는 무중력 상태다. 로켓으로 발사는 했지만 이후 우주에서 추진력 없이 관성으로만 날아가는 우주 탐사선안에서도 무중력 상태다. 이런 우주정거장이나 우주선이 회전하면 그 안에서는 관성력의 하나인 원심력으로 인공중력이 만들어진다. 1968년 영화 <스페이스 오딧세이 2001>를 비롯해 많은 SF영화에 등장해 많이 알려진 방법이다. rpm으로 불리는 분당 회전수가 일정하고 회전 중심에서의 거리가 같으면, 인공중력의 크기도 같다. 인공중력의 방향은 회전 중심에서 멀어지는 방향이다. 인공중력의 크기는 회전 중심에서 멀어질수록 커진다. 회전 중심에서 같은 거리로 만들어지는 모양은 동그라미다. 이런 동그라미 위에서 같이 돌면 바깥방향으로 향하면서 크기는 같은 인공중력을 경험한다. 만약에 우주에서 회전하는 도넛 모양의 구조물 안에 물을 일부 채운다면 어떻게 될까? ‘그림 3’에서처럼 물은 구조물 안의 바깥부분을 동그랗게 채운다. 물 표면이 만드는 모양은 회전하는 방향으로 오목한 모양이다. 다시 말해 수평이 오목한 모양이다. 하지만 회전 축 방향으로는 물표면 또는 수평이 일직선이어서 완전한 오목은 아니고 부분적으로 오목이라고 볼 수 있다.

그림 3. 회전하는 우주정거장 또는 우주선 안에서의 인공중력: 인공중력은 바깥방향으로 향한다. 안에 채워진 물의 수평면은 회전하는 방향으로 오목하다. 이곳에서 평평한 책상을 설치하고 책상 중심을 수평으로 맞추면, 중심에서 회전하는 방향으로 약간만 벗어나도 책상면은 수평이 아니다. 그 곳에 공을 놓으면 회전하는 바깥방향으로 굴러간다.
항상 시민과 함께하겠습니다. 한겨레 구독신청 하기







![[사설] 노동자 안전 뒷전 중대재해법 후퇴가 민생 대책인가 [사설] 노동자 안전 뒷전 중대재해법 후퇴가 민생 대책인가](http://flexible.img.hani.co.kr/flexible/normal/300/180/imgdb/child/2024/0116/53_17053980971276_20240116503438.jpg)

![[올해의 책] 숙제를 풀 실마리를 찾아, 다시 책으로 ①국내서 [올해의 책] 숙제를 풀 실마리를 찾아, 다시 책으로 ①국내서](http://flexible.img.hani.co.kr/flexible/normal/800/320/imgdb/original/2023/1228/20231228503768.jpg)
![[올해의 책] 숙제를 풀 실마리를 찾아, 다시 책으로 ②번역서 [올해의 책] 숙제를 풀 실마리를 찾아, 다시 책으로 ②번역서](http://flexible.img.hani.co.kr/flexible/normal/500/300/imgdb/original/2023/1228/20231228503807.jpg)











